castleman.space
Thomas Castleman's website.
Pyret Moss
2020Pyret Moss is a command-line application for determining similarity between programs written in Pyret, intended for use in plagiarism detection.
The source is here! Created by myself and Raj Paul.
Background
Pyret Moss is inspired by/a derivative of Alex Aiken's "Measure of Software Similarity" system, which runs as a web service and is used by many CS departments to detect cheating in their courses.
The core idea of Aiken's Moss, that of document fingerprinting, is detailed in this paper which we drew from heavily. There is some reference to the actual Moss system at the end of the paper, but it's not much, so we ended up adopting the fingerprinting idea but making up much of the rest of our approach.
Core Idea: Fingerprinting
At the center of the Moss system is its use of the technique of fingerprinting. Essentially, Moss works by:
- Fingerprint submissions
- Hash all substrings of length k in every document
- Algorithmically select some of these hashes to be the "fingerprints" of that document
- Compare fingerprints of each submission. If two submissions share many fingerprints, there is likely significant overlap in their content.
In addition to their substring hash, fingerprints can carry information about what position (whether it be lines/character ranges) in the original text they correspond to. This allows results to point to the specific areas of submissions that were found to be similar, thus alerting the user where to inspect further.
For instance, here's some output from our system:
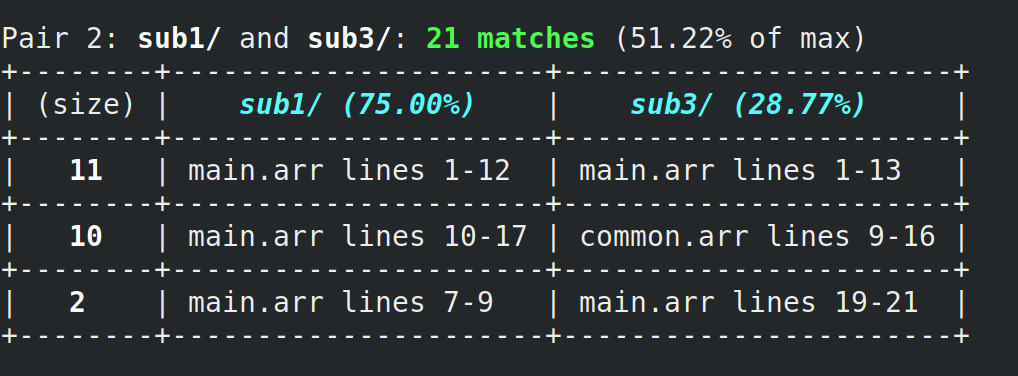
The first row alerts the user that lines 1-12 of main.arr from sub1/ "match" with lines 1-13 of main.arr from sub3/, so they might want to inspect those areas of each submission to determine if plagiarism did indeed occur.
What should be considered similar?
What if I were to take someone else's program, inject whitespace all over, and rename every identifier so the copy bears little resemblance to the original at first glance?
Our system should catch this—and indeed, for this very reason, we have several preprocessing steps in place to "normalize" programs before they are fingerprinted.
Fingerprinting works by hashing substrings, right? So, for plagiarism to be detected, significant amounts of matching substrings must be detected. Therefore, our goal in normalizing has been to immunize the system against any program transformations someone could use to effectively alter the program text in many places (thereby disrupting matching substrings) while not altering the meaning of the program (thereby still reaping the benefits of having copied the work in the first place).
We do this through 5 transformations, all with the intent of eliminating differences between programs that shouldn't be considered important:
| Transformation | Why? |
|---|---|
| Normalize identifiers | So you can't get away with just renaming variables. |
| Remove type annotations | Pyret's type annotations are optional, meaning types could be easily injected/removed, to the detriment of matching substrings. |
| Remove whitespace | Whitespace can also easily be injected (or removed) pretty much anywhere. |
| Remove docstrings | Docstrings are less of a concern due to their more restricted usage, but they still don't affect program meaning and shouldn't differentiate programs. |
| Remove comments | Like whitespace, can be easily injected/removed. |
As an (unrealistically small) example, consider the following two programs:
original.arr
fun evens(l :: List<Number>) -> List<Number>:
doc: "Produces a list of the even numbers in l"
l.filter(lam(n): num-modulo(n, 2) == 0 end)
end
copied.arr
fun only-even-nums(input):
doc: "Get only the evens from the input list"
input.filter(
lam(num :: Number) -> Boolean:
num-modulo(num, 2) == 0
end)
end
The copied.arr version has employed several tricks. However, once normalized, both programs appear identically as:
funv(v):v.v(lam(v):v(v,2)==0end)end
As a result, the copy will likely be detected.
What about presenting overlap?
Once we've determined which pairs of submissions share enough fingerprints for there to be suspicion of plagiarism, we'd like to present this overlap to the user. The goal is, after all, for them to check out more thoroughly the matching spots pointed out by Moss—we just narrow down where to look.
The fact is, however, matching fingerprints just aren't very meaningful to the user. To show overlap in submissions, we could just display each fingerprint that matches and show which parts of files in each submission it matched with, but this leaves much to desire.
Not only could this get unwieldy as the noise/guarantee threshold are tweaked, but by treating the fingerprints in isolation, we're actually ignoring the fact that where and how fingerprints show up is quite important.
Consider for a moment a pair of submissions, A and B:
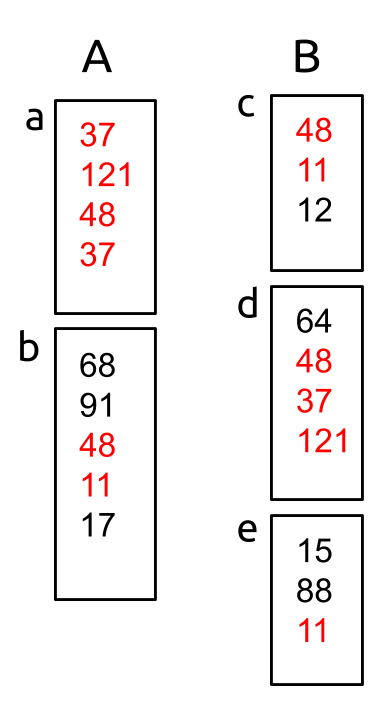
Shared fingerprint hashes are shown in red. You may notice that, in fact, many of the shared fingerprints don't show up alone, but are part of larger substrings that are shared. (If you hover over the above image, you can see some of these shared substrings highlighted)
This is no coincidence: in fact, we expect such substrings to appear in instances of plagiarism. Because fingerprints come from a process of hashing consecutive substrings, if a significant portion of a document has been copied, then we should expect to see not just one, but maybe two or three or many matching fingerprints show up in sequence. The size of such substrings is salient: the longer the substring, the larger the section that has been copied.
So, how do we present overlap to the user?
By analyzing shared substrings of fingerprints, with the goal of upholding the following property:
If a fingerprint is shared, then one of the longest common substrings that includes that fingerprint appears in the output.
Longest common substrings are chosen so that we maximize the matching regions in which each fingerprint is found: the idea is the display each fingerprint in its largest matching context.
(It's important to note here that fingerprints each come from distinct places, and therefore while multiple fingerprints with the same hash may show up in one submission, this does not mean the fact that there are multiple or where they appear isn't important.
For example, consider the two fingerprints in submission B above with hash 11. If we were to report only the substring [48, 11] which includes the 11-fingerprint in document c, we would be leaving out altogether the fact that part of document e matches with document b from submission A. This could be an instance of plagiarism, so it would be unacceptable to omit as such.)
Substring Analysis
How do we identify such substrings between submissions then? Thankfully, the longest common substring problem is plenty well-researched, and can be solved efficiently with dynamic programming.
For our purposes, we want not one longest common substring (LCS), but several, each which are "longest" relative to some shared fingerprint. Three observations come in handy here:
- For all intents and purposes here, a submission is really just a string of the fingerprint hashes that appear in its documents, with the documents delimited somehow (substrings that cross documents aren't meaningful)
- We don't want just one LCS, but hey, the dynamic programming table for LCS computes all common substrings.
- The longest common substring that includes a particular element of either input string can be easily found by examining the row (or column) in which that element occurs.
Convenient! This means we can compute all the information we need to choose substrings by computing the LCS table using as input strings all hashes in A against all hashes in B.
Illustrated:
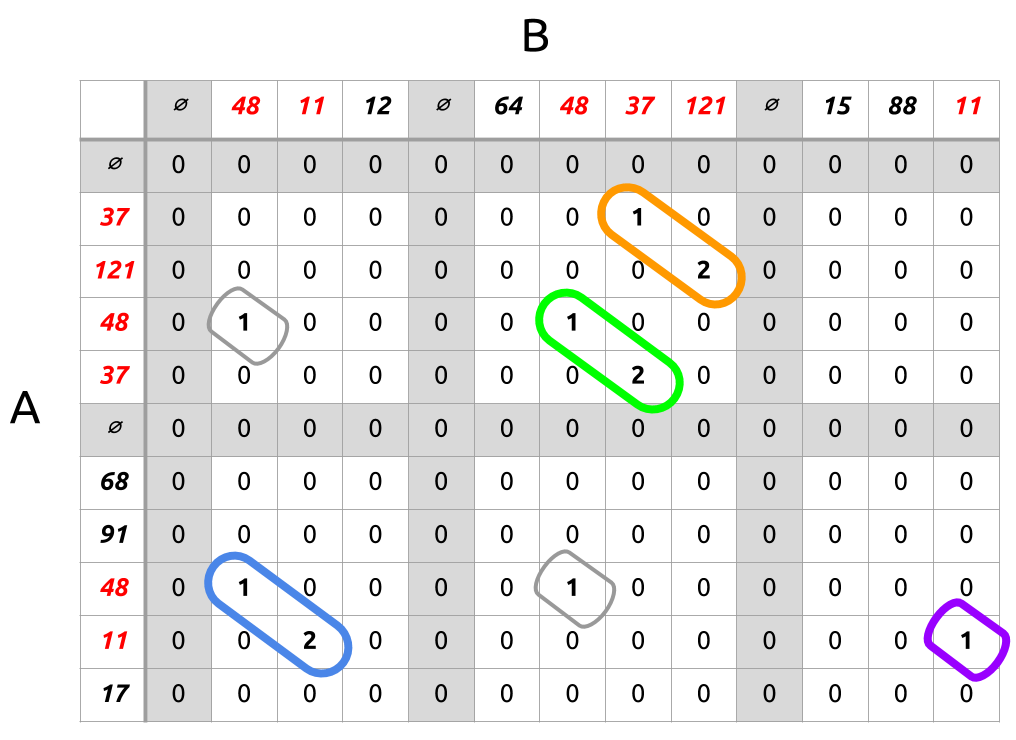
The hashes for A appear along the rows, for B the columns. Documents are delimited by a special symbol, which zeros out its row/column as a special rule to prevent substrings from reaching across document boundaries. Thus each white rectangle cluster of cells between the gray lines can be thought of as a comparison of one document from A with one document from B.
The chosen substrings are shown in orange, green, blue, and purple. These could then be rendered in a table with a description of which line numbers each substring covers, and a note of how long the substring was (its length per se isn't meaningful, but the relative lengths are). This is exactly how we produce our output.